A new shape has been discovered which would make for a pretty unique set of bathroom tiles. Nicknamed “the Hat,” the 13-sided shape can tesselate with itself without ever repeating a pattern, solving a 60-year-old mathematical mystery.
This very niche milestone was made possible by David Smith, a self-proclaimed tiling enthusiast from Yorkshire, England. Along with many others in the community, Smith had been hunting for a specific kind of shape called an aperiodic monotile or an “einstein.” That name has nothing to do with the famous physicist but is instead a play on the German words ein (meaning one) and stein (meaning stone).
This “one stone” is a formerly hypothetical shape that could tile a plane without any overlaps or gaps, and even if it was stretched out over an infinite space would never repeat the same pattern – and physically can’t be made to repeat. Smith’s Hat is the first such shape found to fit the bill.
It might not sound like a big deal for many people, but mathematicians have been searching for a puzzle piece with these properties since the mid-1960s. That’s when the first set of shapes to exhibit aperiodic (non-repeating) tiling was discovered, but the toolbox required over 20,000 different shapes to ensure the pattern never repeated. Further work over the next decade whittled that number down smaller and smaller, until Sir Roger Penrose got it right down to just two, forming arrangements now known as Penrose tilings.
“Those two shapes in Penrose’s solution had enough structure that they forbid periodicity,” said Professor Craig Kaplan, a researcher on a study describing the new shape. “But for almost 50 years mathematicians have been wondering, can we get down to just one shape? Can we do this with a monotile? That’s the problem we solved. We found a single shape that does what all these earlier sets of multiple shapes are able to do.”
Smith had originally been experimenting with paper cutouts of shapes, but there’s only so much you can test with a finite plane. To confirm the Hat’s special abilities, he got in contact with Kaplan, who had recently developed software that could check a given shape on larger scales. For example, it can identify all the different ways the shape can be arranged into small groupings or “neighborhoods,” and then work out if these can exist in a larger tiling without breaking the rules.
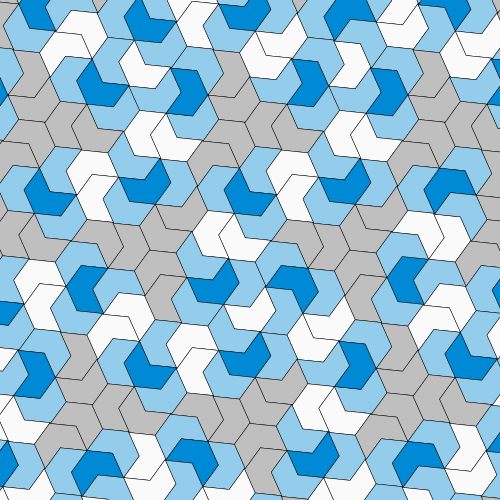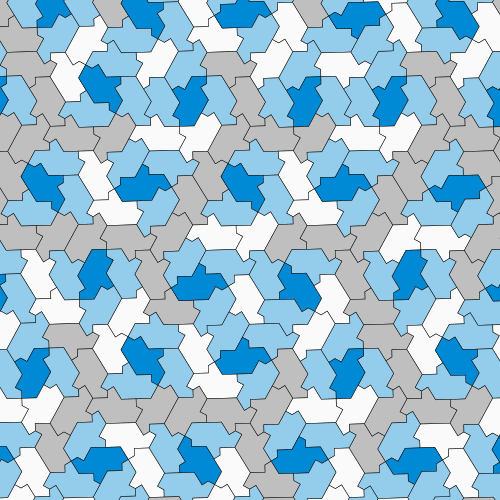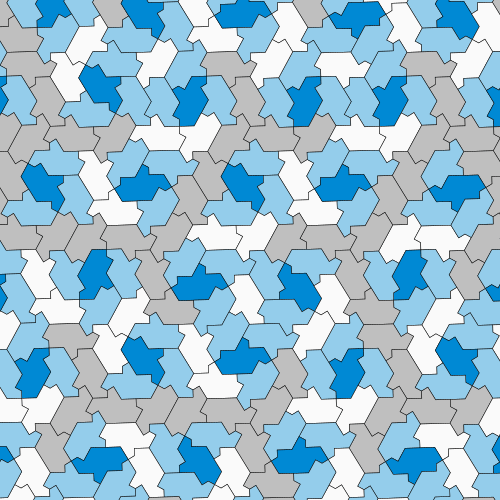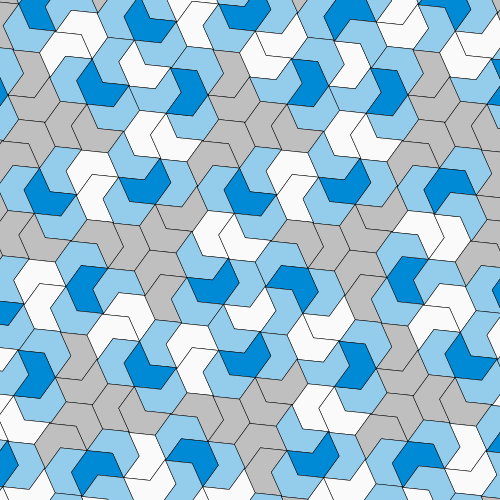
The Hat might not be the only possible aperiodic monotile, either. The team says that technically, it’s part of a family of very similar shapes with slight tweaks that still follow the same rules.
“The more interesting question is are there fundamentally different aperiodic monotiles?” said Kaplan. “My answer is that there’s no reason to suspect otherwise and every reason to suspect there ought to be others.”
Research describing the new shape is available on the preprint server ArXiv.
Source: University of Waterloo




